Question

Prove by induction that for any n≥1n≥1, ∑j=1n(4j 3)=2n2 5n∑j=1n(4j 3)=2n2 5n.

Answer 1

To prove by induction that for any
`\displaystyle\sf n\geq 1`,
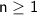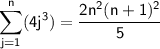`\displaystyle\sf \sum _(j=1)^(n)(4j^(3))=(2n^(2)(n+1)^(2))/(5)`, we will follow the steps of mathematical induction.

Step 1: Base Case

Let's start by verifying the equation for the base case when
`\displaystyle\sf n=1`:

`\displaystyle\sf \sum _(j=1)^(1)(4j^(3))=4(1^(3))=4`

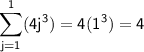
and

`\displaystyle\sf (2(1^(2))(1+1)^(2))/(5)=(2(1)(2)^(2))/(5)=(2(4))/(5)=(8)/(5)=1.6`

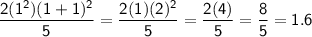
As the equation does not hold for
`\displaystyle\sf n=1`, we cannot consider it as the base case.

Step 2: Inductive Hypothesis

Assume that the equation is true for some positive integer
`\displaystyle\sf k`:

`\displaystyle\sf \sum _(j=1)^(k)(4j^(3))=(2k^(2)(k+1)^(2))/(5)`

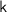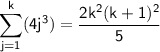
Step 3: Inductive Step

Now we need to prove that the equation holds for
`\displaystyle\sf n=k+1`:

`\displaystyle\sf \sum _(j=1)^(k+1)(4j^(3))=\sum _(j=1)^(k)(4j^(3))+(4(k+1)^(3))`

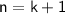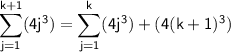
Using the inductive hypothesis:

`\displaystyle\sf =(2k^(2)(k+1)^(2))/(5)+(4(k+1)^(3))`

Simplifying:

`\displaystyle\sf =(2k^(2)(k+1)^(2)+20(k+1)^(3))/(5)`

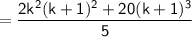
Factoring out
`\displaystyle\sf (k+1)^(2)`:

`\displaystyle\sf =((k+1)^(2)(2k^(2)+20(k+1)))/(5)`

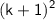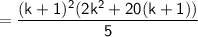
Simplifying further:

`\displaystyle\sf =((k+1)^(2)(2k^(2)+20k+20))/(5)`

`\displaystyle\sf =((k+1)^(2)(2k^(2)+20k+40))/(5)`

`\displaystyle\sf =((k+1)^(2)(2(k^(2)+10k+20)))/(5)`

`\displaystyle\sf =((k+1)^(2)(2(k+5)^(2)))/(5)`

`\displaystyle\sf =(2(k+1)^(2)(k+5)^(2))/(5)`

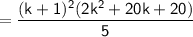
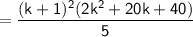
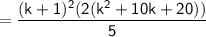
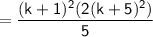
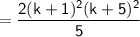
Therefore, the equation holds for
`\displaystyle\sf n=k+1`.

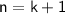Step 4: Conclusion

By the principle of mathematical induction, the equation
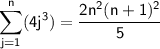`\displaystyle\sf \sum _(j=1)^(n)(4j^(3))=(2n^(2)(n+1)^(2))/(5)` holds for any
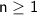`\displaystyle\sf n\geq 1`.