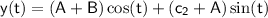Question

Find the general solution of the equation: \[ y^{\prime \prime}+y=2sin (t)+\cos (t)) \]

Answer 1

To find the general solution of the given differential equation
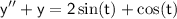`\displaystyle\sf y^(\prime \prime)+y=2\sin (t)+\cos (t)`, we can first solve the associated homogeneous equation
`\displaystyle\sf y^(\prime \prime)+y=0`.

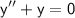The characteristic equation for the homogeneous equation is
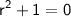`\displaystyle\sf r^(2)+1=0`. Solving this quadratic equation for
`\displaystyle\sf r` yields:

`\displaystyle\sf r^(2)=-1\Rightarrow r=\pm i`

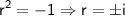
The general solution of the homogeneous equation is then given by:

`\displaystyle\sf y_(h) (t)=c_(1) \cos (t)+c_(2) \sin (t)`

To find a particular solution of the non-homogeneous equation, we assume the form:

`\displaystyle\sf y_(p) (t)=A\sin (t)+B\cos (t)`

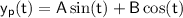
where
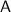`\displaystyle\sf A` and
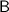`\displaystyle\sf B` are constants to be determined. We substitute this into the differential equation:

`\displaystyle\sf y_(p)^(\prime \prime)+y_(p) =2\sin (t)+\cos (t)`

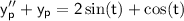
Taking the derivatives and substituting back into the equation, we get:

`\displaystyle\sf (-A\sin (t)-B\cos (t))+A\sin (t)+B\cos (t)=2\sin (t)+\cos (t)`

Simplifying, we have:

`\displaystyle\sf B\cos (t)-B\cos (t)=2\sin (t)+\cos (t)`

which gives:

`\displaystyle\sf 2\sin (t)+\cos (t)=2\sin (t)+\cos (t)`

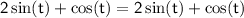
The particular solution
`\displaystyle\sf y_(p) (t)` satisfies the equation. Therefore, we have:

`\displaystyle\sf y_(p) (t)=A\sin (t)+B\cos (t)`

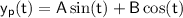
The general solution of the non-homogeneous equation is then given by the sum of the homogeneous and particular solutions:

`\displaystyle\sf y (t)=y_(h) (t)+y_(p) (t)=c_(1) \cos (t)+c_(2) \sin (t)+A\sin (t)+B\cos (t)`

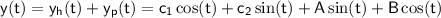
Simplifying, we get:

`\displaystyle\sf y (t)=( A+B) \cos (t)+( c_(2) +A) \sin (t)`

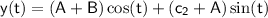
Therefore, the general solution of the given differential equation is:

`\displaystyle\sf y (t)=( A+B) \cos (t)+( c_(2) +A) \sin (t)`