Question

Given the circle below with secant

�
�
�
‾
VUT
and tangent
�
�
‾
ST
, find the length of
�
�
‾
ST
. Round to the nearest tenth if necessary.

Answer 1

ST ≈ 15.3

Explanation:

given a tangent and a secant from an external point to the circle , then

the square of the measure of the tangent is equal to the product of the measures of the secant's external part and the entire secant , that is

ST² = TU × TV = 9 × (9 + 17) = 9 × 26 = 234

take the square root of both sides

ST =
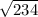`√(234)` ≈ 15.3 ( to the nearest tenth )