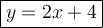Question

Find the equation of the line.
Use exact numbers

Answer 1

to get the equation of any straight line, we simply need two points off of it, let's use those two in the picture below.

`(\stackrel{x_1}{-5}~,~\stackrel{y_1}{-6})\qquad (\stackrel{x_2}{2}~,~\stackrel{y_2}{8}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{8}-\stackrel{y1}{(-6)}}}{\underset{\textit{\large run}} {\underset{x_2}{2}-\underset{x_1}{(-5)}}} \implies \cfrac{8 +6}{2 +5} \implies \cfrac{ 14 }{ 7 } \implies 2`

`\begin{array}c \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-6)}=\stackrel{m}{2}(x-\stackrel{x_1}{(-5)}) \implies y +6 = 2 ( x +5) \\\\\\ y+6=2x+10\implies {\Large \begin{array}{llll} y=2x+4 \end{array}}`

Answer 2

y = 2x + 4

Explanation:

The given graph shows a straight line that intersects the x-axis at (-2, 0) and the y-axis at (0, 4).

Find the slope of the line by substituting the two identified points into the slope formula.

`\textsf{slope}\:(m)=(y_2-y_1)/(x_2-x_1)=(4-0)/(0-(-2))=(4)/(2)=2`

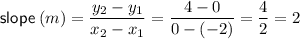
To find the equation of the line, substitute the found slope and y-intercept into the slope-intercept form of a linear equation.

`\boxed{\begin{minipage}{6.3 cm}\underline{Slope-intercept form of a linear equation}\\\\$y=mx+b$\\\\where:\\ \phantom{ww}$\bullet$ $m$ is the slope. \\ \phantom{ww}$\bullet$ $b$ is the $y$-intercept.\\\end{minipage}}`

As m = 2 and b = 4, the equation of the line is:

`\large\boxed{y=2x+4}`