Question

Please help 100 points ​

Answer 1

• vertex: (-5, -6)
• p-value: -1
• opens downward

Explanation:

You want the vertex and p-value for a parabola with focus (-5, -7) and directrix y = -5.

Vertex

The vertex of a parabola is halfway between the focus and directrix. That is because every point on the parabola is the same distance from the focus as from the directrix.

When the vertex is above or below the directrix, it will have the same x-value as the focus. Its y-value will be the average of those of the focus and directrix:

The vertex is ...

(h, k) = (-5, (-7-5)/2)

(h, k) = (-5, -6) . . . . vertex

P-value

The p-value for the parabola is half the distance from the focus to the directrix. When the focus is below the directrix, the p-value is negative.

p = (-7 -(-5))/2 = -1

This is equivalent to the distance from the focus to the vertex.

p = (-7 -(-6)) = -1 . . . . p-value

The sign of the p-value tells you the direction the parabola opens. For negative p-values, the parabola opens downward.

The p-value shows up in the equation for the parabola this way:

`y=(1)/(4p)(x-h)^2+k\qquad\text{vertex at $(h,k)$}`

__

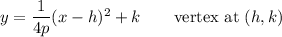
Additional comment

We don't know what your drop-down menu of choices says about the parabola. We have guessed that it might refer to the direction the parabola opens. It always opens in the direction toward the focus and away from the directrix.

<95141404393>