Question

Water leaks out of a tank at a rate of r(t)=10− 3

t 2
​
, measured in gallons per minute. Initially the tank has 70 gallons of water in the tank. How much water is left in the tank after 3 minutes? Provide your answer below: gallons

Answer 1

The amount of water left in the tank after 3 minutes is 21 gallons.

Step-by-step explanation:

To find the amount of water left in the tank after 3 minutes, we need to calculate the integral of the rate function, r(t), from 0 to 3 and subtract it from the initial amount of water in the tank.

The integral of r(t) is given by:

∫(10-3t^2) dt = [10t - (1/3)t^3] evaluated from 0 to 3.

Substituting the values:

[10(3) - (1/3)(3)^3] - [10(0) - (1/3)(0)^3] = 30 - 9 = 21 gallons.

Therefore, there would be 21 gallons of water left in the tank after 3 minutes.

Answer 2

24 gallons of water left in the tank after 3 minutes.

To find out how much water is left in the tank after 3 minutes, you can use the formula for the amount of water remaining in the tank, which is the initial amount minus the integral of the rate of leakage function from 0 to 3 minutes.

The rate of leakage function is given as
`\( r(t) = 13 - (t^2)/(3) \).`

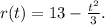
The integral of the rate function gives us the total amount of water that has leaked out from 0 to 3 minutes:

`\[\int_(0)^(3) \left(13 - (t^2)/(3)\right) \, dt\]`

Let's find this integral step by step:

`\[\int_(0)^(3) \left(13 - (t^2)/(3)\right) \, dt = \left[13t - (t^3)/(9)\right]_(0)^(3)\]`

Now, let's substitute the upper and lower limits:

`\[= \left(13 \cdot 3 - (3^3)/(9)\right) - \left(13 \cdot 0 - (0^3)/(9)\right)\]`

Solving this:

`\[= (39 - 3) - (0 - 0) = 36 \text{ gallons}\]`

So, after 3 minutes, 36 gallons of water have leaked out of the tank.

The initial amount in the tank was 60 gallons. Therefore, the amount of water remaining in the tank after 3 minutes is:

Remaining water = Initial amount - Amount leaked

Remaining water = 60 gallons - 36 gallons = 24 gallons

Therefore, after 3 minutes, there are 24 gallons of water left in the tank.

The complete question is here:

Water leaks out of a tank at a rate of
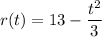`$r(t)=13-(t^2)/(3)$` for
`$t \geq 0$`, measured in gallons per minute. Initially the tank has 60 gallons of water in the tank. How much water is left in the tank after 3 minutes?