Question

Suppose that f(x) is a continuous odd function with ∫06​f(x)dx=−4 What is the value of the integral below? ∫−60​f(x)dx Provide your answer below:

Answer 1

4

Explanation:

You want to know the value of the integral from -6 to 0 of the odd function f(x) if its integral from 0 to 6 is -4.

Odd function

The graph of an odd function is symmetrical about the origin. That is, ...

f(x) = -f(-x)

Area below the x-axis for y > 0 will be above the x-axis for y < 0.

Application

The value of the second integral will be opposite that of the first:

`\displaystyle \int_(-6)^0{f(x)}\,dx=\int_0^(6){f(-x)}\,dx\\\\\\=-\int_0^6{-f(-x)}\,dx=-\int_0^6{f(x)}\,dx\qquad\text{because f(x) is an odd function}\\\\\\=-(-4)=4`

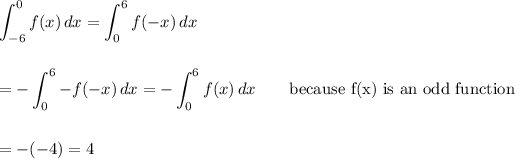
The value of the integral is 4.

<95141404393>