Question

Find the volume of the ellipsoid x 2
+y 2
+7z 2
=25

Answer 1

The volume of the ellipsoid described by the equation
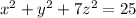`\( x^2 + y^2 + 7z^2 = 25 \)` is approximately 197.90 cubic units.

To find the volume of an ellipsoid given by the equation
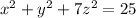`\(x^2 + y^2 + 7z^2 = 25\)`, we can recognize that this is the equation of an ellipsoid centered at the origin with semi-axes
`\(a\)`,
`\(b\)`, and
`\(c\)` in the
`\(x\)`,
`\(y\)`, and
`\(z\)` directions, respectively.

The general form of an ellipsoid's equation is:

`\[(x^2)/(a^2) + (y^2)/(b^2) + (z^2)/(c^2) = 1\]`

Comparing this with the given equation:

`\[x^2 + y^2 + 7z^2 = 25\]`

We can see that:

`\[(x^2)/(5^2) + (y^2)/(5^2) + (z^2)/((√(25/7))^2) = 1\]`

So, the semi-axes are:

`\[a = b = 5, \quad \text{and} \quad c = \sqrt{(25)/(7)}\]`

The volume \(V\) of an ellipsoid is given by the formula:

`\[V = (4)/(3) \pi a b c\]`

Let's substitute the values of \(a\), \(b\), and \(c\) into the formula to find the volume.

The volume of the ellipsoid described by the equation
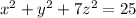`\( x^2 + y^2 + 7z^2 = 25 \)` is approximately 197.90 cubic units.