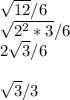Question

How can you write the expression with a rationalized denominator?

((3sqrt2)/(3sqrt6))

A. (3sqrt9)/3

B. ((2+(3sqrt9)))/6

C. (3sqrt9)/6

D. (3sqrt72)/3

I did the math for each one, but none of the answers match

Answer 1

Yeah, The answer I'm getting is sqrt3/3

So yeah, they all seem wrong.

can you check if the question is right??

(the question reduces to sqrt(2)/sqrt(6))

Explanation:

To rationalize, we multiply and divide by the sqrt in the denominator,

(Look at solution to understand this better)

We have,

`3√(2)/3√(6) \\`

In the denominator, we have sqrt6, so we multiply and divide by sqrt6 to rationalize the expression,

`(3√(2) /3√(6) )(√(6) /√(6) )\\= (3√(2)*√(6)/3√(6)*√(6))\\=3√(2*6)/3(√(6*6))\\`

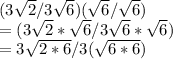
We could have cancelled the 3s at any time, lets do that now,

`3√(2*6)/3(√(6*6))\\√(12)/√(6^2)\\√(12)/6\\`

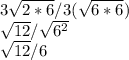
Now, 12 = 4*3 = 2*2*3 = 2^2*3,

`√(12) /6\\√(2^2*3) /6\\2\sqrt3/6\\\\\sqrt3/3`

Answer 2

Answer: D. (3√72)/3

Explanation:

To rationalize the denominator of the expression ((3√2)/(3√6)), we need to eliminate the square root from the denominator. To do this, we can multiply both the numerator and denominator by the conjugate of the denominator, which in this case is √6.

((3√2)/(3√6)) * (√6/√6) = (3√2√6)/(3√6√6) = (3√12)/(3√36)

Simplifying further, we have:

(3√12)/(3√36) = (3√(223))/(3√(6*6))

Now, we can simplify the square roots:

(3√(223))/(3√(66)) = (3√(43))/(3√(66)) = (3√12)/(36)

Canceling out the common factor of 3 in the numerator and denominator, we get:

(√12)/6 = (√(4*3))/6 = (2√3)/6 = (√3)/3

Therefore, the expression with a rationalized denominator is (√3)/3, which corresponds to option D.