The rate of heat flow out of a sphere of radius 1 meter inside a large cube of copper, with thermal conductivity
 kilowatts per meter-kelvin, is approximately
kilowatts per meter-kelvin, is approximately
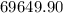 kilowatts.
kilowatts.
To find the rate of heat flow out of a sphere of radius 1 meter inside a large cube of copper, we need to follow these steps:
1. Find the gradient of
 : The temperature distribution within the solid is given by the scalar field
: The temperature distribution within the solid is given by the scalar field
 . The gradient of
. The gradient of
 , denoted
, denoted
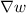 , is a vector field that points in the direction of the greatest rate of increase of the temperature. It can be found by taking the partial derivatives of
, is a vector field that points in the direction of the greatest rate of increase of the temperature. It can be found by taking the partial derivatives of
 with respect to
with respect to
 ,
,
 , and
, and
 .
.
2. **Compute the heat flow vector field
 : The heat flow vector field
: The heat flow vector field
 is given by
is given by
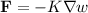 , where
, where
 is the thermal conductivity of copper, which is given as 400 kilowatts per meter-kelvin.
is the thermal conductivity of copper, which is given as 400 kilowatts per meter-kelvin.
3. **Calculate the heat flow across the surface
 : The surface
: The surface
 in this case is the sphere of radius 1 meter. The rate of heat flow out of the sphere is given by the surface integral
in this case is the sphere of radius 1 meter. The rate of heat flow out of the sphere is given by the surface integral
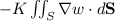 , where
, where
 is a vector representing an infinitesimal element of area on the surface
is a vector representing an infinitesimal element of area on the surface
 , pointing outward.
, pointing outward.
4. Evaluate the surface integral: Since the sphere is symmetric and the temperature distribution is radially symmetric, the gradient
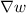 at any point on the sphere will point directly outward. This means that
at any point on the sphere will point directly outward. This means that
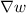 and
and
 are parallel, and the dot product
are parallel, and the dot product
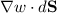 simplifies to
simplifies to
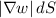 , where
, where
 is the magnitude of
is the magnitude of
 .
.
5. Simplify the integral using symmetry: Due to the symmetry, the magnitude of the gradient
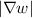 will be the same at all points equidistant from the origin. This allows us to take
will be the same at all points equidistant from the origin. This allows us to take
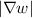 out of the integral and multiply it by the surface area of the sphere,
out of the integral and multiply it by the surface area of the sphere,
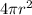 , where
, where
 is the radius of the sphere.
is the radius of the sphere.
Let's start by finding the gradient of
 .
.
The gradient of the temperature function
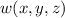 is
is
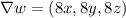 .
.
Next, we'll compute the heat flow vector field
 , which is
, which is
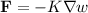 . Given that the thermal conductivity
. Given that the thermal conductivity
 for copper is 400 kilowatts per meter-kelvin, we substitute this into the equation for
for copper is 400 kilowatts per meter-kelvin, we substitute this into the equation for
 .
.
![\[ \mathbf{F} = -400 * (8x, 8y, 8z) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/nd1j8j7x2zzsiynbk4wkeaq7am9i42n7ze.png)
![\[ \mathbf{F} = (-3200x, -3200y, -3200z) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/mjkh18u8q5peu4ztotbngjbr38nnqh6rr5.png)
Now, we'll calculate the rate of heat flow out of the sphere. The surface integral we need to evaluate is:
![\[ -K \iint_S \\abla w \cdot d\mathbf{S} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/aixm6ao4z98i5nvalblk1zjj1ohux55xax.png)
However, since
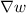 is radially symmetric and points outward, on the surface of the sphere,
is radially symmetric and points outward, on the surface of the sphere,
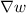 can be replaced by its magnitude at any point on the surface of the sphere, which is at distance 1 from the origin (since the radius of the sphere is 1 meter). The magnitude of the gradient
can be replaced by its magnitude at any point on the surface of the sphere, which is at distance 1 from the origin (since the radius of the sphere is 1 meter). The magnitude of the gradient
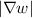 at the surface of the sphere is thus
at the surface of the sphere is thus
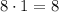 because at the surface
because at the surface
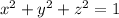 .
.
Let's compute the magnitude of the gradient
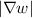 at the surface of the sphere and then proceed to find the rate of heat flow out of the sphere.
at the surface of the sphere and then proceed to find the rate of heat flow out of the sphere.
The rate of heat flow out of a sphere of radius 1 meter inside a large cube of copper, with thermal conductivity
 kilowatts per meter-kelvin, is approximately
kilowatts per meter-kelvin, is approximately
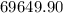 kilowatts.
kilowatts.
the complete Question is given below:
a solid material that has thermal conductivity K in kilowatts per meter-kelvin and temperature given at each point by w(x,y,z)=20−4(x2+y2+z2)οC has heat flow given by the vector field F=−K∇w and rate of heat flow across a surface S within the solid given by −K∫∫S∇wdS.
Find the rate of heat flow out of a sphere of radius 1 meter inside a large cube of copper ( K=400 kilowatts/m-k).