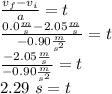Answer:
2.29 s
Step-by-step explanation:
This problem is a description of an elastic collision (the two objects collide and effectively become one object). The equation for an elastic collision is
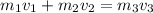 , where:
, where:
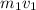 = the mass of the child (55.0 kg) times the velocity of the child (2.5
= the mass of the child (55.0 kg) times the velocity of the child (2.5
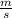 )
)
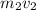 = the mass of the sled (12.0 kg) times the velocity of the sled (0.0
= the mass of the sled (12.0 kg) times the velocity of the sled (0.0
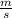 )
)
 = the combined mass of the child and the sled (67.0 kg) times the combined velocity of the child and the sled (
= the combined mass of the child and the sled (67.0 kg) times the combined velocity of the child and the sled (
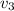 )
)
First, rearrange the problem to solve for
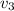 :
:
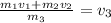
So,
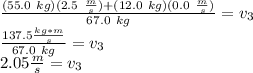
The force of friction for this problem is given as 60 N. To stop the child and the sled, the force of friction must be equal and opposite to the force of the child and sled. According to Newton's first law, force equals mass times acceleration (F=ma). So, an equation to solve this portion of the problem can be given as -60 N=ma, where m=67.0 kg. So,
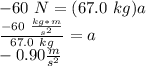
Acceleration can then be used in kinematic equation #1 (
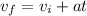 ) to solve for time. Rearrange the equation and let
) to solve for time. Rearrange the equation and let
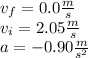
So,