Question

An ideal Otto cycle with a working fluid (cp=1.15 kj/kgoK, cv=0.862 kj/kg0K, R=0.287 kj/kg0K) has an efficiency of 44%. The temperature and pressure at the beginning of compression stage are 200 C and 120 kPa respectively. Determine (a) the maximum temperature and pressure in the cycle, (b) the amount of heat transferred to the air during heat-addition process, and (c) the mean effective pressure. Consider the working fluid as the ideal gas.

Answer 1

In an ideal Otto cycle with the given parameters, the maximum temperature and pressure can be determined using the given information.

The amount of heat transferred to the air during the heat-addition process can be calculated using the efficiency of the cycle. The mean effective pressure, which is a measure of the average pressure exerted on the piston, can also be determined.

The efficiency of the Otto cycle is given by the formula:

η = 1 - (1 / compression ratio)^(γ-1)

Where γ is the ratio of specific heats (cp/cv) and the compression ratio is the ratio of the volume at the beginning of the compression stage to the volume at the end of the compression stage. In this case, the efficiency is given as 0.44, and the ratio of specific heats (γ) can be calculated as cp/cv = 1.15/0.862 = 1.336. Using these values, we can solve for the compression ratio:

0.44 = 1 - (1 / compression ratio)
`^(1.336-1)`

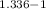
Solving this equation, we find the compression ratio to be approximately 6.198.

The maximum temperature in the cycle occurs at the end of the heat-addition process and can be calculated using the formula:

Tmax = T1 * (compression ratio)
`^(y-1)`

Given that the temperature at the beginning of the compression stage (T1) is 200°C (473K), we can substitute the values to find Tmax.

The maximum pressure in the cycle occurs at the end of the compression process and can be calculated using the ideal gas law:

Pmax = P1 * (compression ratio)^γ

Given that the pressure at the beginning of the compression stage (P1) is 120 kPa, we can substitute the values to find Pmax.

The amount of heat transferred to the air during the heat-addition process can be calculated using the formula:

Qadd = (1 - 1 / (
`compression ratio)^(y-1)`) * cv * T1

Substituting the known values, we can find the heat transferred to the air.

The mean effective pressure (MEP) is defined as the average pressure exerted on the piston during the power stroke of the cycle. It can be calculated using the formula:

MEP = (1 / (compression ratio)^(γ-1)) * P1 * (Tmax - T1)

By substituting the known values, we can find the mean effective pressure.

Learn more about Otto cycle here: