To determine whether the integral
 is convergent or divergent, we can use the p-test for improper integrals.
is convergent or divergent, we can use the p-test for improper integrals.
The p-test states that for the integral
 , it converges if
, it converges if
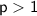 , and it diverges if
, and it diverges if
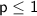 .
.
In our case,
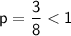 . Therefore, the integral is divergent.
. Therefore, the integral is divergent.
Since the integral is divergent, we do not need to evaluate it.