Question

Over which interval is the graph of f(x) = –x2 + 3x + 8 increasing?

Answer 1

f(x) is increasing for values less than 1.5

or

the interval for which f(x) is increasing is
`(-\infty,1.5)`

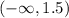
Explanation:

We take the derivative of the function to get,

`f(x) = -x^2 + 3x + 8\\d/dx(f(x)) = d/dx(-x^2+3x+8)\\\\d/dx(f(x)) = -2x+3`

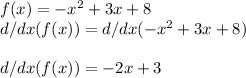
We now have to find when the derivative is zero,

so,

when, -2x+3 = 0

which gives,

-2x+3 = 0

3 = 2x

x=3/2

or, x= 1.5

Now, we need to check the values of the derivative before and after this point,

If the value is positive, then the function is increasing on that side of x = 1.5 and if the value is negative, then the function is decreasing on the side,

So,

value < 1.5

Let's take 1 to be the value,

d/dx[f(1)] = -2(1)+3

= 1

Now, since 1 is positive, f(x) is increasing for values less than 1.5

value >1.5

Let's take 2 to be the value,

d/dx[f(2)] = -2(2)+3

= -1

Now, since -1 is negative, f(x) is decreasing for values greater than 1.5

So, the interval for which f(x) is increasing is , from negative infinity to 1.5