To find the value of
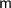 , we can use the slope formula, which states that the gradient (or slope) of a line passing through two points
, we can use the slope formula, which states that the gradient (or slope) of a line passing through two points
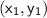 and
and
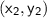 is given by:
is given by:

In this case, we have the following points:
Point P:
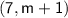
Point Q:
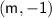
We are given that the gradient of the line is
 . So, we can set up the equation:
. So, we can set up the equation:
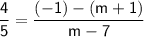
To simplify the equation, we can multiply both sides by
 to eliminate the denominator:
to eliminate the denominator:
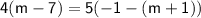
Now, let's solve for
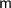 :
:
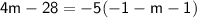
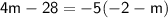
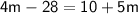
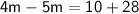
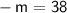

Therefore, the value of
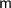 is
is
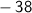 .
.

♥️
