Question

a roller-coaster car is moving at 20 m/s along a straight horizontal track. what will its speed be after climbing the 15-m hill shown in the figure, if friction is ignored?

Answer 1

The speed of the roller-coaster car after climbing the 15-meter hill, if friction is ignored, is approximately 20 m/s.

The speed of the roller-coaster car after climbing the 15-meter hill can be determined using the principle of conservation of mechanical energy.

When the car is at the bottom of the hill, it possesses both kinetic energy (due to its motion) and gravitational potential energy (due to its height above the ground). As the car climbs the hill, its kinetic energy is converted into potential energy. At the top of the hill, all of the car's kinetic energy is converted into potential energy.

To find the speed of the car at the top of the hill, we can equate the initial kinetic energy of the car with the final potential energy of the car.

The initial kinetic energy of the car is given by:

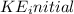`KE_initial` = 1/2 * mass *
`(initial speed)^2`

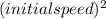
Since the mass of the car is not provided, we can assume it to be constant and cancel it out in the equation.

The final potential energy of the car at the top of the hill is given by:

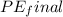`PE_final` = mass * gravity * height

Where "gravity" is the acceleration due to gravity and is approximately equal to 9.8
`m/s^2`.

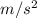Since we are ignoring friction, the loss of mechanical energy due to friction is negligible, and thus we can equate the initial kinetic energy to the final potential energy:

`KE_initial` =
`PE_final`

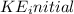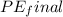
1/2 *
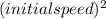`(initial speed)^2` = gravity * height

Substituting the given values, we have:

1/2 *
`(20 m/s)^2` = 9.8 m/s^2
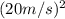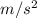`m/s^2` * 15 m

Simplifying the equation:

200
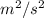`m^2/s^2` = 147
`m^2/s^2`

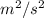
Therefore, the speed of the roller-coaster car after climbing the 15-meter hill, if friction is ignored, is approximately 20 m/s.