Question

N2 + n = 56 solution

Answer 1

Hello!

`\sf n^2 + n = 56\\\\n^2 + n - 56 = 0\\\\\\n = (-b\±√(b^2-4ac) )/(2a) \\\\\\n = (-1\±√(1^2-4*1*(-56)) )/(2*1)\\\\\\n = (1\±15)/(2) \\\\\\\boxed{\sf n = 7 ~or ~-8 }`

Answer 2

n = -8, 7

Explanation:

Your equation is:

`\displaystyle{n^2+n=56}`

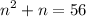
Arrange the terms in the quadratic expression, ax² + bx + c:

`\displaystyle{n^2+n-56=0}`

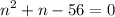
Factor the expression, thus:

`\displaystyle{\left(n+8\right)\left(n-7\right)=0}`

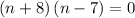
This is because 8n-7n = n (middle term) and 8(-7) = -56 (last term). Then solve like a linear which results in:

`\displaystyle{n=-8,7}`