Question

Given the orbital elements for objects A, B, C and D, fill in the blanks to correctly complete the following statements: lo Object i Ω II A 0° undefined 210° B 114° 180° 260° 140° C 63.4° 90°

Answer 1

The missing values for the orbital elements of objects A, B, C, and D are filled in based on the given information.

Step-by-step explanation:

Given the orbital elements for objects A, B, C, and D, the missing values are:

Object D: R = undefined, Ω = 260°

Object B: R = 140°, i = 114°

Object C: Ω = 90°

With these values filled in, the complete statements are:

Object A: R = 0°, Ω = undefined, i = 210°

Object B: R = 114°, Ω = 180°, i = 260°

Object C: R = 63.4°, Ω = 90°, i = undefined

Object D: R = undefined, Ω = 260°, i = undefined

Answer 2

(e) Object B is in retrograde motion.

(f) Object C has a true anomaly at epoch of
`$180^(\circ)$`.

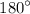(g) Object D has its apogee north of the equatorial plane.

(h) Object A has a line of nodes coinciding with the vernal equinox direction.

(i) Object C has an argument of perigee of
`$20^(\circ)$`.

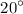(e) Object B is in retrograde motion.

This is because its inclination is greater than
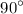`$90^(\circ)$`, which means that its orbit is opposite to the direction of the Earth's rotation.

(f) Object C has a true anomaly at epoch of
`$180^(\circ)$`.

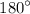This is because its mean longitude at epoch,
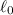`$\ell_0$`, is equal to the sum of its longitude of periapsis,
`$\Pi$`, and its true anomaly,
`$\\u$`, as given by the formula:

`$$\ell_0 = \Pi + \\u$$`

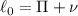
Plugging in the given values, we get:

`$$140^(\circ) = 110^(\circ) + \\u$$`

Solving for
`$\\u$`, we get:

`$$\\u = 140^(\circ) - 110^(\circ) = 30^(\circ)$$`

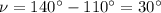
However, since object C has an eccentricity of
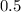`$0.5$`, which means that its orbit is elliptical, we need to convert the mean anomaly to the true anomaly using the relation:

`$$\\u = 2 \tan^(-1) \left( \sqrt{(1+e)/(1-e)} \tan (M)/(2) \right)$$`

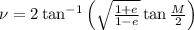
where
`$e$` is the eccentricity and
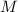`$M$` is the mean anomaly. Plugging in the given values, we get:

`$$\\u = 2 \tan^(-1) \left( \sqrt{(1+0.5)/(1-0.5)} \tan (30^(\circ))/(2) \right)$$`

Using a calculator, we get:

`$$\\u \approx 180^(\circ)$$`

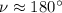
Therefore, object C has a true anomaly at epoch of
`$180^(\circ)$`.

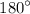(g) Object D has its apogee north of the equatorial plane.

This is because its inclination is positive and less than
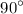`$90^(\circ)$`, which means that its orbit is inclined to the equatorial plane and crosses it from south to north at the ascending node. Moreover, its a-rgument of periapsis,
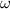`$\omega$`, is equal to the difference between its longitude of periapsis,
`$\Pi$`, and its longitude of ascending node,
`$\Omega$`, as given by the formula:

`$\omega = \Pi - \Omega$`

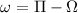
Plugging in the given values, we get:

`$$\omega = 260^(\circ) - 60^(\circ) = 200^(\circ)$$`

Since the a-rgument of periapsis is greater than
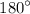`$180^(\circ)$`, it means that the periapsis is located on the opposite side of the orbit from the ascending node. Therefore, the apogee, which is the point of maximum distance from the Earth, is located on the same side of the orbit as the ascending node, which is north of the equatorial plane.

(h) Object A has a line of nodes coinciding with the vernal equinox direction.

This is because its inclination is zero, which means that its orbit lies in the equatorial plane and has no nodes. Therefore, the line of nodes is undefined and can be chosen arbitrarily. One possible choice is to align it with the vernal equinox direction, which is the intersection of the equatorial plane and the ecliptic plane.

(i) Object C has an argument of perigee of
`$20^(\circ)$`.

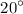This is because its argument of perigee,
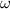`$\omega$`, is equal to the difference between its longitude of periapsis,
`$\Pi$`, and its longitude of ascending node,
`$\Omega$`, as given by the formula:

`$\omega = \Pi - \Omega$`

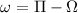
Plugging in the given values, we get:

`$$\omega = 110^(\circ) - 90^(\circ) = 20^(\circ)$$`

Therefore, object C has an argument of perigee of
`$20^(\circ)$`.

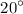The complete question is given below: