Question

A van is traveling due north at a speed of 20 km/h. If the van started off 7 km directly east of the city of Gainesville, how fast, in radians per hour, is the angle opposite the northward path θ changing when the van has traveled 13 km ? (Leave your answer as an exact number.)

Answer 1

To find the rate of change of the angle opposite the northward path, we can differentiate the angle with respect to time.

Step-by-step explanation:

The angle opposite the northward path, in this case, is the angle between the van's path and the direction north. To find this angle, we can create a right triangle with the northward path representing the hypotenuse, the eastward path representing the adjacent side, and the angle opposite the northward path representing the angle θ. Using trigonometry, we can find the angle θ.

Given that the van started off 7 km directly east of Gainesville, we can use the Pythagorean theorem to find the distance traveled north: √(13^2 - 7^2) = √144 = 12 km. Therefore, the angle θ is the arcsin of (12/13), which is approximately 53.13°.

Since we need to find the rate of change of θ with respect to time, we can differentiate with respect to time: dθ/dt = d(arcsin(12/13))/dt.

Answer 2

The angle θ opposite the northward path of the van does not change as the van travels north because the east component of the van's position remains constant relative to the city of Gainesville.

Step-by-step explanation:

To solve this problem, we may use the relationship found in right triangle trigonometry and related rates. When the van has traveled 13 km north, we have a right triangle with one leg (east of city) of 7 km and the hypotenuse (distance from starting point to van's current position) being the sum of 7 km east and 13 km north, which can be calculated using the Pythagorean theorem. Let's denote the angle opposite the northward path as θ. The van's path makes the hypotenuse with the leg that is east of Gainesville.

We find the length of the hypotenuse using the Pythagorean theorem: √(
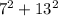`7^(2) + 13^(2)`), which simplifies to √(49 + 169) = √218 km. We denote the distance traveled north as 'y', the original distance east as 'x', and the hypotenuse as 'r'. So, x=7km, y=13km, and r=√218 km. The relationship of the sides and the angle θ is given by the cosine function, cos(θ) = x/r.

To find how fast the angle θ is changing, we need to find dθ/dt. We differentiate both sides of the equation with respect to time 't'. Using the chain rule, the derivative of cos(θ) is -sin(θ)dθ/dt, and the derivative of x/r with respect to time is 0 since x is constant (7 km). Therefore, -sin(θ)dθ/dt = 0, which implies that dθ/dt = 0.

Result: The angle θ is not changing with respect to time as the van travels north because the east component of the van's position does not change, which means the angle formed by the east leg and the hypotenuse of the triangle remains constant.