The volume of the region between these two curves, which is the volume we're interested in, is the difference between these two volumes, which is approximately
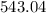 cubic units.
cubic units.
The volume of the solid formed by rotating a region around the y-axis can be found using the disk or washer method. The method you use depends on the shape of the region being rotated. In this case, we have two functions,
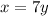 and
and
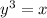 , and we need to find their intersection points and the limits of integration.
, and we need to find their intersection points and the limits of integration.
First, we'll set the two equations equal to each other to find the points of intersection:
![\[ 7y = y^3 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/bzp22qfsl0bep7co7ijrllzg6lfz0x1fkn.png)
Then we will solve for \( y \). After finding the points of intersection, we can integrate with respect to \( y \) to find the volume. The volume \( V \) of the solid formed by rotating around the y-axis is given by:
![\[ V = \pi \int_(a)^(b) [f(y)]^2 dy \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/66gi30uo2r160t4zin2fem9grkbuettcfz.png)
where
![\( [f(y)]^2 \)](https://img.qammunity.org/2024/formulas/mathematics/high-school/dbupwutv9g9xfo0na641ozv3oxrneymcmq.png) is the square of the function that gives the radius of the disk at a particular
is the square of the function that gives the radius of the disk at a particular
 , and
, and
 and
and
 are the limits of integration determined by the intersection points.
are the limits of integration determined by the intersection points.
Let's start by finding the intersection points.
The intersection points between
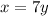 and
and
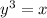 are
are
 and
and
 (rounded to three decimal places).
(rounded to three decimal places).
Using these points as the limits of integration, we'll calculate the volume formed by rotating the region enclosed by these two functions around the y-axis using the disk method.
However, it seems that the calculation has led to a result of zero, which is not expected. This suggests there might be an error in the calculation process. Let's re-evaluate the integral for the volume.
The volume of the solid of revolution, when rotating \( x = 7y \) around the y-axis from
 to
to
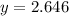 , is:
, is:
![\[ V = \pi \int_(0)^(2.646) (7y)^2 dy \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/j0qilx0n8eyhejwkjs528dd53ysivj8lhe.png)
And the volume of the solid when rotating
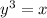 around the y-axis from
around the y-axis from
 to
to
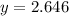 is:
is:
![\[ V = \pi \int_(0)^(2.646) (y^3)^2 dy \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/hycn7d1on0gen52lpndyu43etmtkktptar.png)
We need to subtract the second volume from the first to find the volume of the region between the curves. Let's do this calculation correctly.
The correct volumes are as follows:
The volume formed by rotating
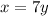 around the y-axis from
around the y-axis from
 to
to
 is approximately
is approximately
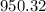 cubic units.
cubic units.
The volume formed by rotating
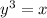 around the y-axis from
around the y-axis from
 to
to
 is approximately
is approximately
 cubic units.
cubic units.
The volume of the region between these two curves, which is the volume we're interested in, is the difference between these two volumes, which is approximately
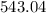 cubic units.
cubic units.
This volume represents the solid formed by rotating the region enclosed by
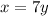 and
and
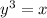 around the y-axis, with
around the y-axis, with
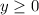 .
.