Question

Which inequality has –12 in its solution set? A B C D x + 6 less-than negative 8 x + 4 greater-than-or-equal-to negative 6 x minus 3 greater-than negative 10 x + 5 less-than-or-equal-to negative 4 A B C D Mark this and return

Answer 1

To find the inequality that has -12 in its solution set, we need to solve each option and see which one includes -12.

Let's go through each option:

A)
`\displaystyle\sf x + 6 < -8`

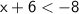
Subtracting 6 from both sides gives us:

`\displaystyle\sf x < -14`

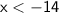
B)
`\displaystyle\sf x + 4 \geq -6x - 3`

Combining like terms and adding 6x to both sides, we get:

`\displaystyle\sf 7x + 4 \geq -3`

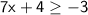
Subtracting 4 from both sides, we have:

`\displaystyle\sf 7x \geq -7`

Dividing by 7, we obtain:

`\displaystyle\sf x \geq -1`

C)
`\displaystyle\sf -6x - 3 > -10`

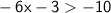
Adding 3 to both sides, we get:

`\displaystyle\sf -6x > -7`

Dividing by -6 and reversing the inequality sign (remembering to flip it when dividing by a negative number), we have:

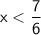
`\displaystyle\sf x < (7)/(6)`

D)
`\displaystyle\sf -10x + 5 \leq -4`

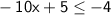
Subtracting 5 from both sides, we obtain:

`\displaystyle\sf -10x \leq -9`

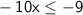
Dividing by -10 and reversing the inequality sign, we have:

`\displaystyle\sf x \geq (9)/(10)`

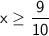
After analyzing the solutions for each option, we find that option A)
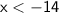`\displaystyle\sf x < -14` is the one that includes -12 in its solution set.

Therefore, the inequality that has -12 in its solution set is
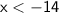`\displaystyle\sf x < -14`.