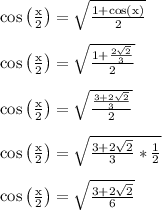Question

Find the exact value of cos x/2 if sin x=5/15 and 180° is greater than or equal to x ≥ 90°

show your work please

thank you​

Answer 1

Answer:
`\sqrt{(3+2√(2))/(6)}`

============================================

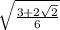
Step-by-step explanation

"180° is greater than or equal to x ≥ 90°" is the same as writing
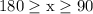`180 \ge \text{x} \ge 90` which is the same as
`90 \le \text{x} \le 180`

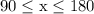
The angle x is in quadrant Q2 where cosine is negative and sine is positive

sin(x) = 5/15 = 1/3

`\cos^2(\text{x})+\sin^2(\text{x}) = 1\\\\\cos^2(\text{x}) = 1-\sin^2(\text{x})\\\\\cos^2(\text{x}) = 1-\left((1)/(3)\right)^2\\\\\cos^2(\text{x}) = (8)/(9)\\\\\cos(\text{x}) = -\sqrt{(8)/(9)} \ \ \text{.... cos is negative in Q2}\\\\\cos(\text{x}) = -(√(8))/(√(9))\\\\\cos(\text{x}) = -(2√(2))/(3)\\\\`

---------

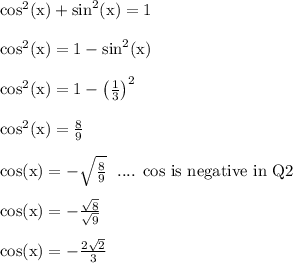
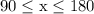`90 \le \text{x} \le 180` leads to
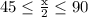`45 \le \frac{\text{x}}{2} \le 90` after dividing all sides by 2.

The angle x/2 is between 45 and 90, which places it in quadrant Q1 or on the positive y axis. If
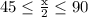`45 \le \frac{\text{x}}{2} \le 90` then
`\cos\left(\frac{\text{x}}{2}\right) \ge 0`

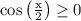
We'll use a trig identity to compute cos(x/2).

`\cos\left(\frac{\text{x}}{2}\right) = \sqrt{\frac{1+\cos(\text{x})}{2}}\\\\\cos\left(\frac{\text{x}}{2}\right) = \sqrt{(1+(2√(2))/(3))/(2)}\\\\\cos\left(\frac{\text{x}}{2}\right) = \sqrt{((3+2√(2))/(3))/(2)}\\\\\cos\left(\frac{\text{x}}{2}\right) = \sqrt{(3+2√(2))/(3)*(1)/(2)}\\\\\cos\left(\frac{\text{x}}{2}\right) = \sqrt{(3+2√(2))/(6)}\\\\`