To factor the expression
 , we can first identify that it is a polynomial with two terms. Notice that both terms have a common factor of
, we can first identify that it is a polynomial with two terms. Notice that both terms have a common factor of
 . Factoring out
. Factoring out
 , we have:
, we have:
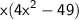 .
.
Now, we can observe that the expression
 is a difference of squares. It can be rewritten as
is a difference of squares. It can be rewritten as
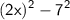 . Applying the formula for factoring a difference of squares, we obtain:
. Applying the formula for factoring a difference of squares, we obtain:
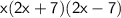 .
.
Therefore, the completely factored form of
 is
is
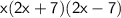 .
.