Answer:
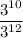
Explanation:
You want to identify the expression that is equivalent to 3^(-2).
Rules of exponents
The relevant rule of exponents is ...
(a^b)/(a^c) = a^(b-c)
Application
This means you want to find the expression such that subtracting the bottom exponent from the top one yields -2.
(3^-2)/(3^3) = 3^(-2-3) = 3^-5 . . . . . not equivalent
(3^10)/(3^-12) = 3^(10 -(-12)) = 3^22 . . . . . not equivalent
(3^3)/(3^22) = 3^(3-22) = 3^-19 . . . . . . not equivalent
(3^10)/(3^12) = 3^(10-12) = 3^-2 . . . . . equivalent
__
Additional comment
If you consider that an exponent signifies repeated multiplication, you can see how this works.
3^5 = 3×3×3×3×3
3^3 = 3×3×3
Then (3^5)/(3^3) = (3×3×3×3×3)/(3×3×3) = 3×3 = 3^2
This is the same as 3^(5-3) = 3^2.
That is, the denominator exponent is subtracted from the numerator exponent. This shows you where the subtraction comes from.
As with many models, representation of negative numbers is not so easy. That doesn't mean the rule is not applicable. It just means it is somewhat more difficult to show with a physical representation.
<95141404393>