Question

NO LINKS!! URGENT HELP PLEASE!!

For #22-24
Find the volume of each figure. Round answers to the nearest hundredth.​

Answer 1

22) 576 cm³

23) 74.67 ft³

24) 374.4 m³

Explanation:

The volume of a pyramid is the product of the area of its base and a third of its height:

`\boxed{V=(1)/(3)hA_(\sf base)}`

`\hrulefill`

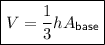
Question 22

The diagram shows a pyramid with a square base, with side length s = 12 cm and height h = 12 cm.

The area of a square is the square of its side length, s². Therefore:

`\begin{aligned}\sf Volume_(\sf pyramid)&=(1)/(3)hA_(\sf base)\\\\&=(1)/(3)hs^2\\\\&=(1)/(3)\cdot 12 \cdot 12^2\\\\&=(1)/(3)\cdot 12 \cdot 144\\\\&=4 \cdot 144\\\\&=576\; \sf cm^3\end{aligned}`

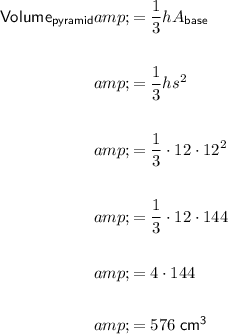
Therefore the volume of the square-based pyramid is 576 cm³.

`\hrulefill`

Question 23

The diagram shows a pyramid with a rectangular base, with side lengths w = 4 ft and l = 8 ft, and height h = 7 ft.

The area of a rectangle is the product of its width and length. Therefore:

`\begin{aligned}\sf Volume_(\sf pyramid)&=(1)/(3)hA_(\sf base)\\\\&=(1)/(3)hwl\\\\&=(1)/(3)\cdot 7 \cdot 4 \cdot 8\\\\&=(7)/(3)\cdot 4 \cdot 8\\\\&=(28)/(3) \cdot 8\\\\&=(224)/(3)\\\\&=74.67\; \sf ft^3\end{aligned}`

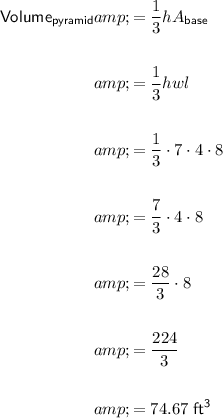
Therefore the volume of the square-based pyramid is 74.67 ft³, rounded to the nearest hundredth.

`\hrulefill`

Question 24

The diagram shows a pyramid with a regular hexagonal base, with side length s = 6 m, apothem a = 5.2 m, and height h = 12 m.

The area of a regular polygon is:

`\boxed{A=(n\:s\:a)/(2)}`

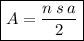
where:

• n = number of sides
• s = length of one side
• a = apothem

Therefore:

`\begin{aligned}\sf Volume_(\sf pyramid)&=(1)/(3)hA_(\sf base)\\\\&=(1)/(3)h\left((n\:s\:a)/(2)\right)\\\\&=(1)/(3)(12)\left((6 \cdot 6 \cdot 5.2)/(2)\right)\\\\&=4\left((187.2)/(2)\right)\\\\&=4\left(93.6\right)\\\\&=374.4\; \sf m^3\end{aligned}`

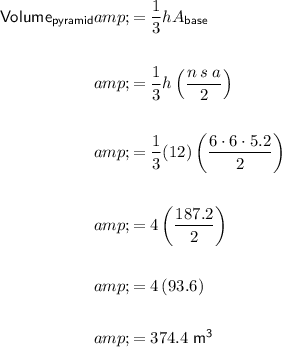
Therefore the volume of the square-based pyramid is 374.4 m³.

Answer 2

22. 576 cm³

23. 74.67 ft³

24. 374.12 m³

Explanation:

22.

Volume of square pyramid: ⅓*area of base* height

here

area of base= area of square =Length²=12²=144cm²

height=12cm

substituting value in above formula

Volume of square pyramid: ⅓*144*12=576 cm³

23.

Volume of rectangle pyramid: ⅓*area of base* height

here

area of base= area of rectangle =Length*breadth

=4*8=32 ft²

height=7ft

substituting value in above formula

Volume of rectangle pyramid: ⅓*32*7=74.67 ft³

24.

Volume of hexagon pyramid: ⅓*area of base* height

here

area of base= area of hexagon =
`(3*√(3))/(2)*side^2`==
`(3*√(3))/(2)*6^2`=93.53 m²,

height=12 m

substituting value in above formula

Volume of square pyramid: ⅓*93.53*12=374.12 m³