Question

NO LINKS!!! URGENT HELP PLEASE!!!

20. Find the volume of the figure. Round answer to the nearest hundredth.​

Answer 1

996 in³

Explanation:

The given figure is a regular pentagonal prism.

To find its volume, we first need to find the area of its pentagonal base.

From inspection of the given diagram, the parameters of the pentagonal base are:

• Side length, s = 12 in
• Apothem, a = 8.3 in
• Number of sides, n = 5

Substitute these values into the area of a regular polygon formula to find the area of the base of the prism.

`\boxed{\begin{minipage}{6cm}\underline{Area of a regular polygon}\\\\$A=(n\cdot s\cdot a)/(2)$\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the length of one side.\\ \phantom{ww}$\bullet$ $a$ is the apothem.\\\end{minipage}}`

Therefore:

`\begin{aligned}\textsf{Base\;area}&=(5 \cdot 12 \cdot 8.3)/(2)\\\\&= (498)/(2)\\\\&=249\; \sf in^2\end{aligned}`

To find the volume of the prism, multiply the base area by the prism's height:

`\begin{aligned}\textsf{Volume}&=\sf Base\;area * height\\\\&=249 * 4\\\\&=996\; \sf in^3\end{aligned}`

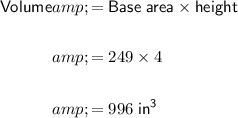
Therefore, the volume of the prism is 996 in³.

Answer 2

996 in³

Explanation:

Volume of pentagon pyramid:5/2*apothem*side* height

here

apothem =8.3 in

height =4 in

side length=12 in

Now

substituting value in above formula

Volume of pentagon pyramid:5/2*8.3*4*12=996 in³