Answer:

Explanation:
Quadratic formula
The quadratic formula is a mathematical formula used to solve quadratic equations. It provides the solutions for an equation of the form ax² + bx + c = 0, where a, b, and c are constants, and x represents the variable.
The quadratic formula is given by:
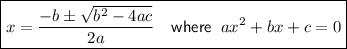

Given quadratic equation:

To solve the given quadratic equation using the quadratic formula, first identify the coefficients a, b, and c in the given equation:
Substitute the values of a, b, and c into the quadratic formula and solve for x:
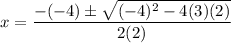
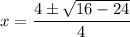
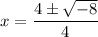
Since the expression under the square root is negative, we have complex solutions:
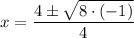
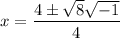
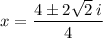
Simplify by dividing the numerator and denominator by 2:


Solutions
Therefore, the solutions to the equation 2x² - 4x + 3 = 0 are:
