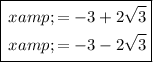Question

Solve the equation x^2 + 6x - 3 = 0 by completing the square

Answer 1

Answer: X1= -2
`√(3)` -3 , X2= 2
`√(3)` -3

Explanation:

Answer 2

`x=-3+2√(3)`

`x=-3-2√(3)`

Explanation:

To solve the equation x² + 6x - 3 = 0 by completing the square, first move the constant term to the right side of the equation by adding 3 to both sides:

`x^2 + 6x = 3`

Add the square of half of the coefficient of x to both sides of the equation:

`x^2 + 6x + \left((6)/(2)\right)^2 = 3 + \left((6)/(2)\right)^2`

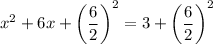
Simplify:

`x^2 + 6x + \left(3\right)^2 = 3 + \left(3\right)^2`

`x^2 + 6x + 9 = 3 + 9`

`x^2 + 6x + 9 = 12`

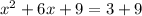
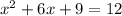
Factor the left side of the equation:

`(x + 3)^2 = 12`

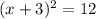
Square root both sides of the equation:

`√((x + 3)^2) = \pm √(12)`

`x+3= \pm √(12)`

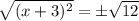
Subtract 3 from both sides of the equation to isolate x:

`x=-3 \pm √(12)`

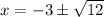
Simplify √(12):

`x=-3 \pm √(2^2 \cdot 3)`

`x=-3 \pm √(2^2) √(3)`

`x=-3 \pm 2√(3)`

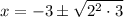
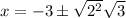
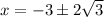
Therefore, the solutions to the equation are:

`\boxed{\begin{aligned}x&=-3+ 2√(3)\\x&=-3-2√(3)\end{aligned}}`