Question

Graph the porabola please put the dots on the graph that i provided 100points

Answer 1

Vertex = (1, -6)

Focus = (2, -6)

Explanation:

The standard form of a sideways parabola that opens left to right is:

`\boxed{(y-k)^2=4p(x-h)}`

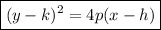
where:

• p > 0
• Vertex = (h, k)
• Focus = (h+p, k)
• Directrix: x = (h - p)
• Axis of symmetry: y = k

Given equation:

`(x-1)=((y+6)^2)/(4)`

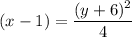
Rearrange the given equation so that it is in standard form by multiplying both sides by 4:

`4 \cdot (x-1)=4 \cdot ((y+6)^2)/(4)`

`4(x-1)=(y+6)^2`

`\boxed{(y+6)^2=4(x-1)}`

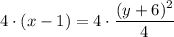
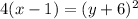
Comparing it with the standard form (y - k)² = 4p(x - h):

• h = 1
• k = -6
• p = 1

Therefore:

• Vertex = (1, -6)
• Focus = (1+1, -6) = (2, -6)
• Directrix: x = (1 - 1) = 0
• Axis of symmetry: y = -6

The vertex is the point where the curve changes direction. In a sideways parabola opening to the right, it is the point furthest to the left.

In a sideways parabola, the axis of symmetry is a horizontal line that passes through the vertex. This line divides the parabola into two symmetrical halves, and it is parallel to the x-axis.

The focus is a point that lies on the axis of symmetry and is equidistant from all points on the parabola. It is located inside the curve, so in a sideways parabola opening to the right, it is to the right of the vertex.

The directrix is a line perpendicular to the axis of symmetry. It is a vertical line located outside the curve and is equidistant from all the points on the parabola. In a sideways parabola opening to the right, it is to the left of the vertex.

To plot the graph using your graphical calculator, move the vertex to point (1, -6). The other point (focus) should be at (2, -6).

Plot:

• Vertex = (1, -6)
• Focus = (2, -6)
• Directrix: x = 0
• Axis of symmetry: y = -6