Answer:
To determine if the two triangles are similar, we can compare their corresponding angles and side lengths.
Let's compare the corresponding angles of the two triangles:
So, in triangle ABC:
Angle ABC is a right angle (90 degrees) since it's formed by a line perpendicular to the river and the river bank. Angle BAC is the angle we are standing at, which we'll call angle 1.
In triangle CDE: Angle CDE is a right angle (90 degrees) since it's formed by a line perpendicular to the river and the river bank. Angle DCE is the same angle as angle 1 since they are alternate interior angles (which is formed by a transversal intersecting two parallel lines). Right now, we can see that the two triangles have ONE pair of congruent angles (90 degrees) and one pair of corresponding angles (Angle 1 and DCE) that are equal.
Now, let's compare the corresponding side lengths of the two triangles:
In triangle ABC:
Side AB is the distance across the river that we need to calculate. Side BC is the distance you walked downstream, which is 16 feet.
In triangle CDE:
Side CE is the distance you walked away from the river, which is 9 feet. Side DE is the distance between the third and fourth poles, which is 7 feet.
We can see that the ratios of the corresponding side lengths are:
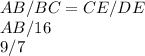
To know if the triangles are similar, we need the ratios of the corresponding side lengths to be equal. To solve for the unknown side length, we need to do AB:

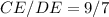
Cross-multiplying, we have: AB * 7 = 16 * 9AB = (16 * 9) / 7AB ≈ 20.57 feet. So, the distance across the river (side AB) is approximately 20.57 feet. In conclusion:
1. The two triangles, ABC and CDE, are similar because they have one pair of congruent angles (90 degrees) and one pair of corresponding angles (1 and DCE) that are equal.
This similarity is based on the Angle-Angle (AA) similarity theorem.
2. The distance across the river (side AB) is approximately 20.57 feet, calculated using proportions based on the similarity of the triangles.
I hope this helps :)