Question

{(-2,1),(3,1),(2,1),(4,1),(-3,1)}

Is the relation a fuction?

The domain is { }.
The range is { }.

Answer 1

To determine if the relation is a function, we need to check if each input (x-value) corresponds to a unique output (y-value).

The given relation is: {(-2,1),(3,1),(2,1),(4,1),(-3,1)}

Since every input value has the same output value of 1, it means that each input maps to a unique output. Hence, this relation is a function.

Now let's determine the domain and range of this function.

Domain:

The domain is the set of all possible input values (x-values). In this case, the x-values in the relation are -2, 3, 2, 4, and -3. Therefore, the domain is:

`\displaystyle\sf \text{{Domain}} = \{-2, 3, 2, 4, -3\}`

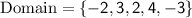
Range:

The range is the set of all possible output values (y-values). In this case, the y-value in the relation is always 1. Therefore, the range is:

`\displaystyle\sf \text{{Range}} = \{1\}`

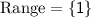
So, the domain of the function is {-2, 3, 2, 4, -3}, and the range is {1}.