Let's assume the measure of each exterior angle of the regular polygon is
 .
.
According to the given information, the measure of each interior angle is three times the measure of each exterior angle. Therefore, the measure of each interior angle is
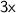 .
.
In a regular polygon, the sum of all interior angles is given by the formula
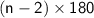 , where
, where
 is the number of sides of the polygon.
is the number of sides of the polygon.
Since each interior angle measures
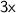 , the sum of all interior angles can also be expressed as
, the sum of all interior angles can also be expressed as
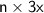 .
.
Setting these two expressions equal to each other, we can write the equation:

Now, we can solve for
 , the number of sides of the polygon.
, the number of sides of the polygon.
Dividing both sides of the equation by
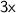 :
:

Simplifying:
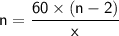
This equation shows that the number of sides
 is proportional to
is proportional to
 . We need more information, specifically the value of
. We need more information, specifically the value of
 , to determine the exact number of sides of the polygon.
, to determine the exact number of sides of the polygon.