To solve the system of equations:

There are multiple methods to solve this system, such as substitution, elimination, or using matrices. Let's solve it using the elimination method.
We can eliminate one variable by multiplying both sides of the second equation by 5:

Now, we have the equations:

Next, subtract the second equation from the first equation to eliminate
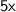 :
:

Simplifying further:
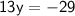
Now, solve for
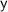 by dividing both sides of the equation by 13:
by dividing both sides of the equation by 13:
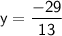
Thus, we have found the value of
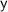 to be
to be
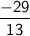 .
.
To find the value of
 , substitute the value of
, substitute the value of
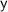 into one of the original equations. Let's use the first equation:
into one of the original equations. Let's use the first equation:
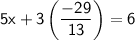
Now, solve for
 :
:
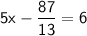
Add
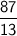 to both sides:
to both sides:
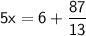
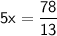
Finally, divide both sides by 5 to isolate
 :
:
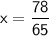
Therefore, the solution to the system of equations is
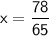 and
and
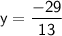 .
.