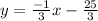Question

.QUESTIONS The equation of a circle is x² + y² -8x+6y=15.

5.1. prove that the point (2:-9) is on the circumference of the circle.

5.2. Determine an equation of the tangent to the circle at the point (2; -9), (7) [9]​

Answer 1

1) See below

2)
`y = (-1)/(3)x -(25)/(3)`

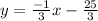
Explanation:

1) x² + y² - 8x + 6y = 15

⇒ x² + y² - 8x + 6y - 15 = 0

If the point (x = 2, y = -9) lises on the circle, then it should satisfy the above equation

Substituting the values in the equation,

2² + (-9)² - 8(2) + 6(-9) - 15

= 4 + 81 - 16 - 54 - 15

= 0

The point (2, -9) satisfies the equation of the circle

Therefore, the point lies on the circle

2)

The general equation of a circle is :

x² + y² - 2ax - 2by + a² + b² - r² = 0 where (a, b) is the centre of the circle

Comaring this with the equation of our circle,

we have :

-2ax = -8x ,

-2by = 6y

⇒ a = -8x / (-2a),

b = 6y / (-2b)

⇒ a = 4,

b = -3

centre: (4, -3)

We have m₁m₂ = -1

⇒ m₁ = -1/m₂

where m₁ is the gradient of the tangent and m₂ is the gradient of the diammeter (which is perpendicular to the tangent)

We have points on the diammeter: (x₁ = 4, y₁ = -3) (x₂ = 2, y₂ = -9)

`m_2 = (y_2 - y_1)/(x_2 - x_1) \\\\= (-9 +3)/(2-4)\\ \\=(-6)/(-2)\\ \\= 3`

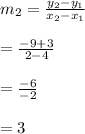
m₁ = -1/3

Equation of tangent:

y = m₁x + c

We have point of tanget: (2, -9) and m₁ = -1/3

so,

-9 = (-1/3)*(2) + c

c = -9 + 2/3

c = -25/3

Eq of tangent:

`y = (-1)/(3)x -(25)/(3)`