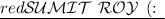Question

Simplify : sin theta{1/sin theta- 1/cosec theta}

Answer 1

To simplify the expression
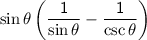`\displaystyle\sf \sin\theta \left( (1)/(\sin\theta) - (1)/(\csc\theta) \right)`, we can start by simplifying the denominator terms.

Recall that
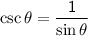`\displaystyle\sf \csc\theta = (1)/(\sin\theta)`. Substituting this into the expression, we have:

`\displaystyle\sf \sin\theta \left( (1)/(\sin\theta) - (1)/((1)/(\sin\theta)) \right)`

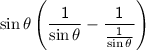
Simplifying further:

`\displaystyle\sf \sin\theta \left( (1)/(\sin\theta) - (1)/((1)/(\sin\theta)) \right) = \sin\theta \left( (1)/(\sin\theta) - (\sin\theta)/(1) \right)`

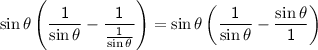
Combining the fractions:

`\displaystyle\sf \sin\theta \left( (1 - \sin\theta)/(\sin\theta) \right)`

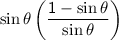
Canceling out the common factor of
`\displaystyle\sf \sin\theta`:

`\displaystyle\sf (1 - \sin\theta)/(\sin\theta)`

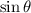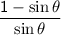
Therefore, the simplified expression is
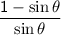`\displaystyle\sf (1 - \sin\theta)/(\sin\theta)`.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`