Question

The perimeter of a rectangular swimming pool is 154m.its lengh is 2m more than twice its breadth.what is the length and breadth of the pool (also find the equation and use transpose method)​

Answer 1

Let's denote the length of the pool as L and the breadth as B.

According to the given information, the perimeter of the rectangular swimming pool is 154m. The formula for the perimeter of a rectangle is given by:

`\displaystyle\sf P = 2(L + B)`

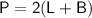
Substituting the given value of the perimeter, we have:

`\displaystyle\sf 154 = 2(L + B)`

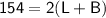
Dividing both sides of the equation by 2, we get:

`\displaystyle\sf 77 = L + B`

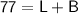
We are also given that the length of the pool is 2m more than twice its breadth. Mathematically, we can express this as:

`\displaystyle\sf L = 2B + 2`

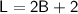
Now we can substitute this value of L in terms of B into the equation we obtained earlier:

`\displaystyle\sf 77 = (2B + 2) + B`

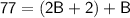
Simplifying the equation, we have:

`\displaystyle\sf 77 = 3B + 2`

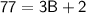
Subtracting 2 from both sides of the equation, we get:

`\displaystyle\sf 75 = 3B`

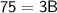
Dividing both sides of the equation by 3, we obtain:

`\displaystyle\sf B = 25`

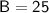
Now we can substitute this value of B into the equation for L:

`\displaystyle\sf L = 2(25) + 2`

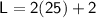
Simplifying the equation, we have:

`\displaystyle\sf L = 52`

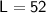
Therefore, the length of the pool is 52m and the breadth is 25m.

Using the transpose method, we can rearrange the equation
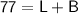`\displaystyle\sf 77 = L + B` to solve for L:

`\displaystyle\sf L = 77 - B`

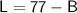
Then, substituting this expression for L in the equation
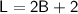`\displaystyle\sf L = 2B + 2`, we have:

`\displaystyle\sf 77 - B = 2B + 2`

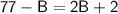
Adding B to both sides of the equation, we get:

`\displaystyle\sf 77 = 3B + 2`

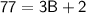
Subtracting 2 from both sides of the equation, we obtain:

`\displaystyle\sf 75 = 3B`

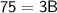
Finally, dividing both sides of the equation by 3, we find:

`\displaystyle\sf B = 25`

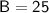
By substituting this value of B back into the equation
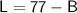`\displaystyle\sf L = 77 - B`, we get:

`\displaystyle\sf L = 77 - 25 = 52`

Hence, the length of the pool is 52m and the breadth is 25m.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`