Question

Express 0.3333 in the form of p/q in it's simplest form
​

Answer 1

To express 0.3333 as a fraction in its simplest form
`\displaystyle\sf (p)/(q)`, we can start by setting
`\displaystyle\sf x = 0.3333`.

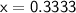To eliminate the decimal, we multiply both sides of the equation by 10000 (since there are four decimal places in 0.3333) to get
`\displaystyle\sf 10000x = 3333.3`.

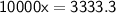Next, we simplify the equation by dividing both sides by 10000, which gives
`\displaystyle\sf x = (3333.3)/(10000)`.

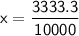To further simplify this fraction, we can divide both the numerator and the denominator by their greatest common divisor (GCD). In this case, the GCD of 3333.3 and 10000 is 3333.3.

Dividing both the numerator and the denominator by 3333.3, we obtain
`\displaystyle\sf x = (3333.3)/(10000) = (3333.3 / 3333.3)/(10000 / 3333.3) = (1)/(3)`.

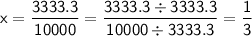Hence, 0.3333 can be expressed as
`\displaystyle\sf (1)/(3)` in its simplest form.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`