To find the possible values of m, we can use the distance formula in a coordinate plane. The distance between two points (x₁, y₁) and (x₂, y₂) is given by:
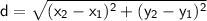
In this case, we have the point P(m, 4) and the point Q(-3, -1), and the distance between them is 5√5. Plugging the values into the formula, we get:
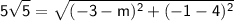
Simplifying the equation, we have:

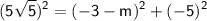
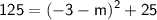
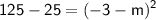

Taking the square root of both sides, we get:
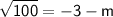 or
or
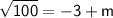
Simplifying further, we have two possibilities:
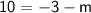 or
or
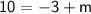
For the first equation, solving for m, we have:
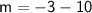
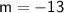
For the second equation, solving for m, we have:
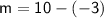
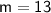
Therefore, the possible values of m are
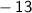 and
and
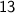 .
.

♥️
