Question

Then find the . f(x/y) = (9/16) ^ - 3 / ((9/16) ^ - 2) value of * (x/y) ^ - 1 + (y/x) ^ - 1​

Answer 1

To simplify the expression
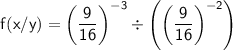`\displaystyle\sf f(x/y) = \left((9)/(16)\right)^(-3) / \left(\left((9)/(16)\right)^(-2)\right)` and find the value of
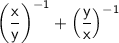`\displaystyle\sf \left((x)/(y)\right)^(-1) + \left((y)/(x)\right)^(-1)`, we can begin by evaluating each component separately.

Let's simplify
`\displaystyle\sf \left((9)/(16)\right)^(-3)`:

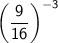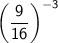`\displaystyle\sf \left((9)/(16)\right)^(-3)` can be rewritten as
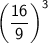`\displaystyle\sf \left((16)/(9)\right)^(3)`. Taking a number to the power of -n is equivalent to taking its reciprocal and raising it to the power of n:

`\displaystyle\sf \left((16)/(9)\right)^(3) = \left((9)/(16)\right)^(-3)`.

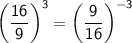So,
`\displaystyle\sf \left((9)/(16)\right)^(-3) = \left((16)/(9)\right)^(3)`.

Next, let's simplify
`\displaystyle\sf \left((9)/(16)\right)^(-2)`:

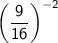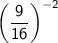`\displaystyle\sf \left((9)/(16)\right)^(-2)` can be rewritten as
`\displaystyle\sf \left((16)/(9)\right)^(2)`:

`\displaystyle\sf \left((9)/(16)\right)^(-2) = \left((16)/(9)\right)^(2)`.

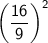Now, let's evaluate
`\displaystyle\sf \left((x)/(y)\right)^(-1) + \left((y)/(x)\right)^(-1)`:

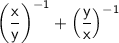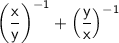`\displaystyle\sf \left((x)/(y)\right)^(-1) + \left((y)/(x)\right)^(-1)` is equivalent to
`\displaystyle\sf (1)/(\left((x)/(y)\right)) + (1)/(\left((y)/(x)\right))`.

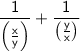Simplifying this expression further:

`\displaystyle\sf (1)/(\left((x)/(y)\right)) + (1)/(\left((y)/(x)\right)) = (y)/(x) + (x)/(y)`.

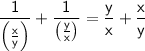To simplify the overall expression
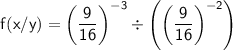`\displaystyle\sf f(x/y) = \left((9)/(16)\right)^(-3) / \left(\left((9)/(16)\right)^(-2)\right)`, we substitute the simplified values:

`\displaystyle\sf f(x/y) = \left((16)/(9)\right)^(3) / \left((16)/(9)\right)^(2)`.

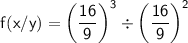When dividing with the same base raised to different exponents, we can subtract the exponents:

`\displaystyle\sf f(x/y) = \left((16)/(9)\right)^(3-2)`.

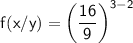Simplifying further:

`\displaystyle\sf f(x/y) = \left((16)/(9)\right)^(1)`.

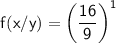Finally, we get
`\displaystyle\sf f(x/y) = (16)/(9)`.

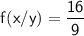And
`\displaystyle\sf (y)/(x) + (x)/(y) = (y^2 + x^2)/(xy)`.

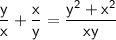So the expression
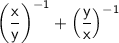`\displaystyle\sf \left((x)/(y)\right)^(-1) + \left((y)/(x)\right)^(-1)` simplifies to
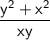`\displaystyle\sf (y^2 + x^2)/(xy)`.