Question

An equation is shown: x2 + 4x + 4 = 0

What are the x intercepts? Show your work using a method of your choice.


What is an alternate method you could use to find the x intercepts (other than the method you used)?


What is the vertex? Is it a minimum or maximum? How do you know by looking at the equation?


What steps would you take to graph using the information you have already calculated? How would you use symmetry to help you graph?

Answer 1

x-intercept: x = -2

Alternative method: Quadratic formula

Vertex: (-2, 0)

Minimum as the leading coefficient is positive.

Explanation:

x-intercepts

The x-intercepts are the points at which the curve crosses the x-axis, so the x-values when y = 0.

As the quadratic equation is already equal to zero, to find the x-intercepts, factor and solve for x.

`x^2+4x+4=0`

`x^2+2x+2x+4=0`

`x(x+2)+2(x+2)=0`

`(x+2)(x+2)=0`

`(x+2)^2=0`

`(x+2)=0`

`x=-2`

Therefore, the x-intercept of the given quadratic equation is x = -2.

`\hrulefill`

Alternative method

An alternative method to use to find the x-intercept(s) is the quadratic formula.

`\boxed{\begin{minipage}{4 cm}\underline{Quadratic Formula}\\\\$x=(-b \pm √(b^2-4ac))/(2a)$\\\\\\when $ax^2+bx+c=0$ \\\end{minipage}}`

`\hrulefill`

Vertex

The vertex of a quadratic function is the turning point of the parabola. It is the point where the graph reaches its minimum or maximum value

As there is only one x-intercept of the given quadratic equation, and the equation can be rewritten in the form (x + 2)² = 0, we can identify that the vertex of the parabola is the x-intercept, (-2, 0).

Since the leading coefficient of the equation is positive, the parabola opens upwards. Therefore, the vertex represents a minimum.

`\hrulefill`

Graphing

The graph of a quadratic equation is a parabola.

A parabola is symmetric with respect to its axis of symmetry, which is a vertical line passing through its vertex. As the vertex of the given quadratic equation is (-2, 0), the axis of symmetry is x = -2.

To graph the equation using the information already calculated, first plot the vertex at (-2, 0) and draw the axis of symmetry through the vertex.

Find other points on the graph by inputting values of x into the function f(x) = x² + 4x + 4, then reflect those points across the axis of symmetry.

By connecting these points and considering the symmetry, we can sketch the graph of the equation.

Answer 2

x intercepts are (-2, 0).

Explanation:

X intercepts: The x intercepts are the points where the graph of the equation crosses the x-axis. In order to find the x intercepts, we can set the equation equal to 0 and solve for x.

x^2 + 4x + 4 = 0

(x + 2)^2 = 0

x + 2 = 0

x = -2

Therefore, the x intercepts are (-2, 0).

`\hrulefill`

Alternate method: Another method to find the x intercepts is to use the quadratic formula. The quadratic formula is:

`x = (-b \± √(b^2 - 4ac))/(2a)`

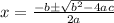
Comparing x^2 + 4x + 4 = 0 with ax^2=bx+c=0,

In this case, we get a = 1, b = 4, and c = 4.

Substituting these values into the quadratic formula, we get:

`x = (-4 \± √(4^2 - 4 * 1 * 4) )/(2 * 1)\\x =(-4)/(2)\\x=-2`

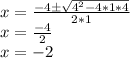
Therefore, the x intercepts are still (-2, 0).

`\hrulefill`

Vertex: The vertex is the point of the parabola that is highest or lowest.

In order to find the vertex, we can use the formula:

`(h, k) = ((-b)/(2a), (-(b^2-4ac))/(4a))`

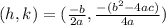
Comparing x^2 + 4x + 4 = 0 with ax^2=bx+c=0,

In this case, we get a = 1, b = 4, and c = 4.

Substituting these values into the formula, we get:

`(h, k) = ((-4)/(2*1), (-(4^2-4*1*4))/(4*1))\\(h, k) =(-2,0)`

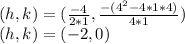
Therefore, the vertex is (-2, 0).

Minimum or maximum: The vertex is a minimum because the coefficient of x^2 is positive. This means that the parabola opens upwards, and the vertex is the lowest point of the parabola.

`\hrulefill`

Graphing: In order to graph the equation, we can first plot the x intercepts.

Graph: Attachment

Then, we can draw a parabola that passes through the x intercepts and the vertex. We can use symmetry to help us graph the parabola.

The graph can be drawn by inputting values of x into the function f(x) = x² + 4x + 4,

The parabola is symmetric about the vertical line that passes through the vertex. This means that if we reflect the parabola over this line, we will get the same parabola.

As you can see, the parabola opens upwards and has a minimum vertex at (-2, 0).