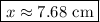Question

Find x please and show step by step and proofing as well thankyou ​

Answer 1

`x \approx 7.68 \text{ cm}`

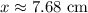
Explanation:

We can solve for the length of segment x in this circle diagram by using the principles of tangency and the altitude of a right triangle.

First, we can assume that the hypotenuse of the diagrammed right triangle is tangent to, or parallel with, the circumference of the circle at its point of intersection it. This means that it is perpendicular, or at a right angle, to the radius at the point of intersection with the circumference.

Second, we can see that the altitude of the diagrammed right triangle is the radius of the circle which intersects with the circumference at the hypotenuse's point of tangency (see the attached image).

We can use our knowledge of a right triangle's altitude to make the assertion that the three triangles formed by drawing the altitude are all similar. This means that their angles are the congruent.

We can solve for the length of the horizontal segment
`h` (the hypotenuse of one of the triangles formed by drawing the altitude) by using the trigonometric ratio cosine.

`\cos(\theta) = \frac{\text{adjacent}}{\text{hypotenuse}}`

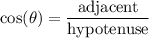
↓ plugging in the known values

`\cos(52\°) = (6)/(h)`

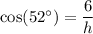
↓ dividing both sides by 6

`(\cos(52\°))/(6) = \frac{1}h`

↓ taking the reciprocal of both sides

`h = (6)/(\cos(52\°))`

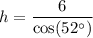
Finally, we can solve for x by constructing another right triangle, assuming that the segment of length x is tangent to the circle's circumference. We know that the sides of the right triangle are: the radius,
`h`, and x. We already know two of these values (the radius and
`h`), so we can solve for x using the Pythagorean Theorem.

`a^2 + b^2 = c^2`

↓ plugging in the known values

`x^2 + 6^2 = \left((6)/(\cos(52\°))\right)^2`

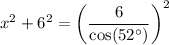
↓ subtracting 6² from both sides

`x^2 = \left((6)/(\cos(52\°))\right)^2 - 6^2`

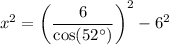
↓ taking the square root of both sides

`x = \sqrt{\left((6)/(\cos(52\°))\right)^2 - 6^2}`

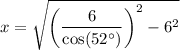
↓ evaluating using a calculator

`\boxed{x \approx 7.68\text{ cm}}`

Answer 2

x ≈ 7.68

Explanation:

You want to find the length x of the tangent segment in the given figure.

Triangles

Drawing an altitude of the triangle to the upper point of tangency, we have the figure shown in the first attachment. All of these right triangles are similar, so ∠CAB ≅ ∠CDA = 52°.

Tangent

The tangent of the angle 52° is given by ...

Tan = Opposite/Adjacent

tan(52°) = BC/BA

The tangents to the circle from point C are the same length, so BC = x and ...

tan(52°) = x/6

x = 6·tan(52°) ≈ 7.68 . . . . cm

The value of x cm is about 7.68 cm.

<95141404393>