To find the magnitude and direction of the electric field, we can use the equation for the Lorentz force
 experienced by a charged particle moving in a magnetic field:
experienced by a charged particle moving in a magnetic field:
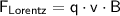 ,
,
where
 is the Lorentz force,
is the Lorentz force,
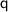 is the charge of the particle,
is the charge of the particle,
 is the velocity of the particle, and
is the velocity of the particle, and
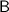 is the magnetic field.
is the magnetic field.
In this case, the Lorentz force
 is given as
is given as
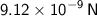 , the charge
, the charge
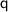 is
is
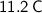 , and the velocity
, and the velocity
 is
is
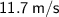 .
.
We can rearrange the equation to solve for the magnitude of the magnetic field
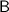 :
:
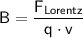 .
.
Substituting the given values, we have
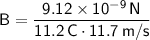 .
.
Calculating this, we find
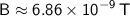 .
.
Therefore, the magnitude of the magnetic field is
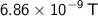 .
.
To determine the direction of the electric field, we need to consider the Lorentz force equation:
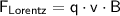 .
.
The Lorentz force is perpendicular to both the velocity
 and the magnetic field
and the magnetic field
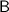 . Given that the particle is moving toward the geographic West, the magnetic field
. Given that the particle is moving toward the geographic West, the magnetic field
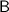 must be directed downward (toward the Earth's surface) to exert a force towards the East (perpendicular to the velocity).
must be directed downward (toward the Earth's surface) to exert a force towards the East (perpendicular to the velocity).
Therefore, the direction of the electric field is downward.

♥️
