a) To find the acceleration of the masses and the tension in the string, we need to consider the forces acting on the system.
1. Forces on m1 (block on the ramp):
- - Weight (mg1) acting vertically downward.
- - Normal force (N1) perpendicular to the ramp.
- - Frictional force (f) opposing the motion.
The component of the weight acting parallel to the incline is
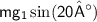 , and the component perpendicular to the incline is
, and the component perpendicular to the incline is
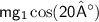 .
.
The normal force
 is equal in magnitude and opposite in direction to the perpendicular component of the weight, so
is equal in magnitude and opposite in direction to the perpendicular component of the weight, so
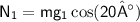 .
.
The frictional force
 is given by
is given by
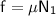 , where
, where
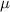 is the coefficient of kinetic friction.
is the coefficient of kinetic friction.
The net force acting on m1 is the force parallel to the incline, which is the difference between the weight component and the frictional force:
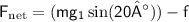 .
.
Using Newton's second law
 , where
, where
 is the acceleration of the masses, we can find the acceleration:
is the acceleration of the masses, we can find the acceleration:
 .
.
Now, let's consider the forces acting on m2 (hanging block):
- - Weight (mg2) acting vertically downward.
- - Tension (T) in the string, which is acting vertically upward.
Since the two blocks are connected by the string, the tension in the string is the same for both blocks, so
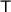 is the tension in the string.
is the tension in the string.
Using Newton's second law for m2, we have:
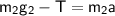 .
.
Now we have two equations with two unknowns (a and T). Solving these equations simultaneously will give us the values for acceleration and tension.
b) To find the maximum value of m2 that will not make m1 slide up the incline, we need to consider the forces and the maximum static friction.
When m1 is at the verge of sliding up the incline, the force of static friction
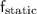 is at its maximum and is given by
is at its maximum and is given by
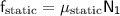 , where
, where
 is the coefficient of static friction.
is the coefficient of static friction.
The force of static friction
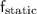 must be equal to or greater than the component of the weight of m1 parallel to the incline, which is
must be equal to or greater than the component of the weight of m1 parallel to the incline, which is
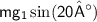 .
.
So we have:
 .
.
Using the expression for
 from part a, we can substitute and solve for the maximum value of m2.
from part a, we can substitute and solve for the maximum value of m2.