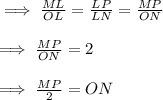Answer:
1) a) ∠MOS = 62
b) ∠MLP = 31
Explanation:
1)
a) Chord MS creates an angle of ∠MTS = 31 at a point on the circle
∠MOS is the angle created by chord MS at the centre
Therefore,
∠MOS = 2*∠MTS
= 2*31
=62
∠MOS = 62
b) Since PM = MS, the angle created by these chords are the same
∠MLP = ∠MTS
∠MLP = 31
2) Prove that ON = MS/2
Since MS = MP,
we need to prove that ON = MP/2
We have OL = OM = radius
OL + OM = ML
ML = 2*OL -eq(1)
Since ON bisects LP,
LN = NP
LP = LN + NP
LP = 2*LN -eq(2)
Consider ΔMLP and ΔOLN
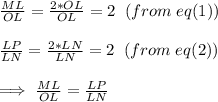
Also ∠MLP = ∠OLN = 31
By SAS property, ΔMLP and ΔOLN are similar