Question

Find the pythagorean triplets for the following values of 'n'. N=1 N=2 N=3 N=4

PLS HELP FAST!!! ​

Answer 1

The triplets generated are,

(3,4,5), (6,8,10), (8,15,17), (5,12,13), (12,16,20), (7,24,25)

Note: to check which triplet is generated with what value of n, look at solution (e.g, (3,4,5) is generated with n= 1 and n =2 (or p =2,q=1))

Explanation:

To generate the pythagorean triples for the values, we use the following formulas,

a = p^2 - q^2

b = 2pq

c = p^2 + q^2

Where p > q

Now, we have 4 values, 1, 2, 3, 4,

We have to calculate all the combinations, so,

The combinations involving n = 1 are,

Since 1 is the smallest integer, we get,

p = 2, q = 1

`a = 2^2 - 1^2\\b = 2(2)(1)\\c = 2^2 + 1^2\\so,\\a = 4-1\\b=4\\c=4+1\\Hence,\\a=3\\b=4\\c=5`

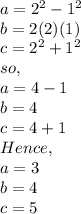
the first triplet is, (for p =2 ,q =1) (3,4,5)

p=3, q =1

Again using the formulas to find a,b,c

`a = 3^2 - 1^2b = 2(3)(1)c = 3^2 + 1^2\\a = 8\\b=6\\c=10`

So for p=3,q=1, the triple is (6,8,10) or (8,6,10)

p = 4 , q = 1

`a = 4^2 - 1^2\\b = 2(4)(1)\\c = 4^2 + 1^2\\\\a=15\\b=8\\c=17`

Hence we get the triplet (8,15,17)

for p = 3, q = 2

`a = 3^2 - 2^2\\b = 2(3)(2)\\c = 3^2 + 2^2\\\\a=9-4\\b=12\\c=9+4\\\\a=5\\b=12\\c=13`

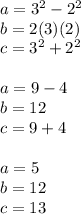
So, the triplet is (5,12,13)

for p = 4, q = 2,

`a = 4^2 - 2^2\\b = 2(4)(2)\\c = 4^2 + 2^2\\\\a=16-4\\b=16\\c=16+4\\\\a=12\\b=16\\c=20`

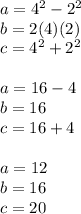
The triplet is (12,16,20)

Finally,

for p = 4, q = 3

`a = 4^2 - 3^2\\b = 2(4)(3)\\c = 4^2 + 3^2\\\\a=16-9\\b=24\\c=16+9\\\\a=7\\b=24\\c=25`

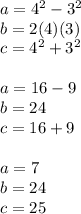
So, the triplet is (7,24,25)