Question

Prove Co = AB + C¡ (A ⊕ B) = BC¡＋AC¡ + AB​

Answer 1

To prove the equation
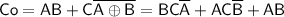`\displaystyle\sf Co = AB + C\overline{A \oplus B} = BC\overline{A} + AC\overline{B} + AB`, we will manipulate the given expression using Boolean algebra laws and logic operations.

Starting with the left-hand side of the equation:

`\displaystyle\sf AB + C\overline{A \oplus B}`

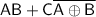
We can expand the term
`\displaystyle\sf C\overline{A \oplus B}` using the XOR operation:

`\displaystyle\sf C\overline{(A \cdot \overline{B} + \overline{A} \cdot B)}`

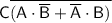
Applying De Morgan's law to the expression inside the complement:

`\displaystyle\sf C\overline{(A \cdot \overline{B}) \cdot (\overline{A} \cdot B)}`

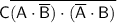
Distributing the complement over the product:

`\displaystyle\sf C(\overline{A \cdot \overline{B}} + \overline{\overline{A} \cdot B})`

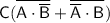
Using De Morgan's law again:

`\displaystyle\sf C(\overline{A} + B) \quad (1)`

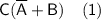
Now, let's simplify the right-hand side of the equation:

`\displaystyle\sf BC\overline{A} + AC\overline{B} + AB`

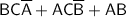
Factoring out A from the second term and B from the third term:

`\displaystyle\sf (BC + AC)\overline{A} + AB`

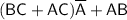
Applying the distributive law:

`\displaystyle\sf (B + A)C\overline{A} + AB`

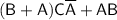
Using the absorption law, which states that
`\displaystyle\sf X + XY = X`:

`\displaystyle\sf BC\overline{A} + AB`

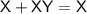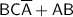
Comparing the right-hand side expression with the expression (1) derived from the left-hand side, we can see that they are equal.

Therefore, we have proven that
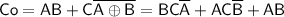`\displaystyle\sf Co = AB + C\overline{A \oplus B} = BC\overline{A} + AC\overline{B} + AB`.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`