Answer:
27.8 cm
Explanation:
The question asks us to calculate the hypotenuse of a right-angled triangle whose height is 14 cm and whose area is 168 cm².
To do this we have to first calculate the length of the base of the triangle, which is labelled in the diagram attached below.
In order to calculate the length of the base, we have to use the formula for the area of a triangle:

⇒
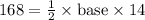
⇒
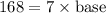
⇒
 [Dividing both sides of the equation by 7]
[Dividing both sides of the equation by 7]
⇒
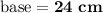
Now that we have the length of the base, we can use the Pythagorean Theorem to calculate the hypotenuse:
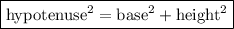
⇒
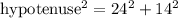
⇒
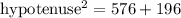
⇒

⇒
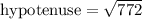 [Taking the square root of both sides]
[Taking the square root of both sides]
⇒
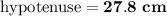
Therefore, the hypotenuse of the triangle is 27.8 cm.