Question

11 The Sum 3 Consecutive numbers. L is 27, hund the greatest number.​

Answer 1

To find the sum of three consecutive numbers, we can use the formula:

`\displaystyle\sf \text{{Sum}} = \frac{{\text{{First number}} + \text{{Last number}}}}{2} * \text{{Number of terms}}`.

In this case, we are given that the sum of the three consecutive numbers is 27, so we have:

`\displaystyle\sf 27 = \frac{{\text{{First number}} + \text{{Last number}}}}{2} * 3`.

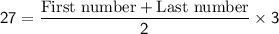Simplifying, we have:

`\displaystyle\sf 27 = \frac{{\text{{First number}} + \text{{Last number}}}}{2} * 3`.

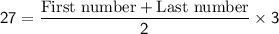Multiplying both sides by 2:

`\displaystyle\sf 54 = (\text{{First number}} + \text{{Last number}}) * 3`.

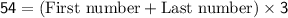Dividing both sides by 3:

`\displaystyle\sf 18 = \text{{First number}} + \text{{Last number}}`.

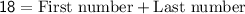Since the numbers are consecutive, we can express the first number in terms of the last number as follows:

`\displaystyle\sf \text{{First number}} = \text{{Last number}} - 2`.

Substituting this expression into the equation above, we get:

`\displaystyle\sf 18 = (\text{{Last number}} - 2) + \text{{Last number}}`.

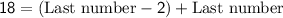Simplifying:

`\displaystyle\sf 18 = 2 * \text{{Last number}} - 2`.

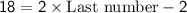Adding 2 to both sides:

`\displaystyle\sf 20 = 2 * \text{{Last number}}`.

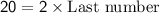Dividing both sides by 2:

`\displaystyle\sf 10 = \text{{Last number}}`.

Therefore, the greatest number is 10.