Question

Sophia has 5 cards numbered 1,3,5,7,9
how many 3 digit numbers divisible by 3 can she make?

Answer 1

Sophia has 5 cards numbered 1, 3, 5, 7, and 9. To form a 3-digit number, the number formed should be divisible by 3.

For a number to be divisible by 3, the sum of its digits must be divisible by 3. In this case, Sophia needs to select three cards from the given set and form a number.

To calculate the number of 3-digit numbers divisible by 3, we can use the concept of combinations. The total number of combinations of selecting 3 cards out of 5 is given by the formula
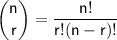`\displaystyle\sf \binom{n}{r}=(n!)/(r!(n-r)!)`, where
`\displaystyle\sf n` is the total number of items and
`\displaystyle\sf r` is the number of items to be selected.

Using this formula, the number of ways Sophia can select 3 cards out of the given 5 is
`\displaystyle\sf \binom{5}{3}=(5!)/(3!(5-3)!)`.

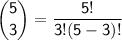Simplifying, we have
`\displaystyle\sf \binom{5}{3}=(5* 4* 3!)/(3!* 2!)`.

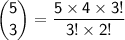Canceling out the common terms, we get
`\displaystyle\sf \binom{5}{3}=(5* 4)/(2* 1)=10`.

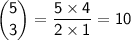So, Sophia can make 10 different 3-digit numbers using the given cards.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`