Question

You want to buy a house that costs $230,000. You will make a down payment equal to 10 percent of the price of the house and finance the remainder with a loan that has an APR of 5.27 percent compounded monthly. If the loan is for 20 years, what are your monthly mortgage payments?

Answer 1

$1,397.17

Explanation:

To calculate the monthly mortgage payments, we need to determine the loan amount after the down payment and then use Monthly Payment Formula to calculate the monthly payments.

Monthly Payment Formula

`\boxed{PMT=(PVi\left(1+i\right)^n)/(\left(1+i\right)^n-1)}`

where:

• PMT = Monthly payment.
• PV = Loan amount.
• i = Interest rate per month (in decimal form).
• n = Term of the loan (in months).

If the house costs $230,000, and a down payment equal to 10% of the price of the house is made, then the value of the loan (PV) is:

`PV=230000 \cdot 90\%=\$207,000`

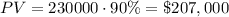
If the APR is 5.27%, then the value of i is:

`i = (0.0527)/(12)`

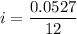
If the term of the loan is 20 years, then the value of n is:

`n = 20 \cdot 12 = 240 \; \sf months`

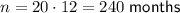
Substitute the values into the formula:

`PMT=(207000 \cdot (0.0527)/(12)\left(1+(0.0527)/(12)\right)^(240))/(\left(1+(0.0527)/(12)\right)^(240)-1)`

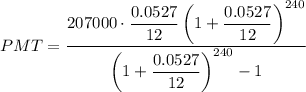
Using a calculator to evaluate, we get:

`PMT=1397.17122...`

`PMT=1397.17`

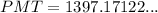
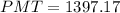
Therefore, the monthly mortgage payment would be approximately $1,397.17 (to the nearest cent).